ダイレクトコンバージョン方式のSDRなどではRF信号をAD変換する前段で直交ミキサによる周波数変換を行う。今回はこの直交ミキサをCMOSアナログスイッチで実現するための原理について調べ、LTSpiceで回路を組んでシミュレーションによる動作確認を行った。
CMOSアナログスイッチを用いた直交ミキサ回路はネット上でチラホラ見かけるものの、動作原理を解説した記事が殆ど無く、特に日本語の記事は皆無だったため頑張って海外の文献を紐解いて理解するようにした。
そういうわけで、今回はやや専門的な内容が含まれており趣味のブログの域を少々逸脱している気もするのだが、周波数変換回路を理解する上で基礎となる大事な所なので、難しくなりすぎないよう心がけつつ記事にまとめた。
CMOSアナログスイッチを用いた周波数変換の原理
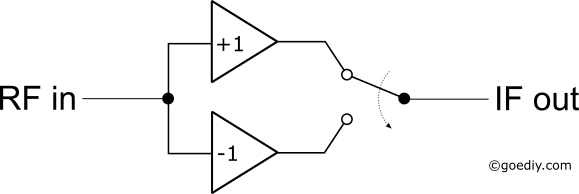
周波数変換回路の詳細はADI社のチュートリアル(英語)に理論も含めて解説されている。要するにRF信号にサイン波を乗算すると周波数が変換されるという事で、真面目にアナログ乗算器ICを使っても良いが、もっと簡単にスイッチを使ってミキサ回路を構成することが出来ると紹介されている。スイッチが+1倍と-1倍の乗算器を一定の周波数で交互に切り替えることで、矩形波の乗算器を通したのと等価な結果が得られるということだ。
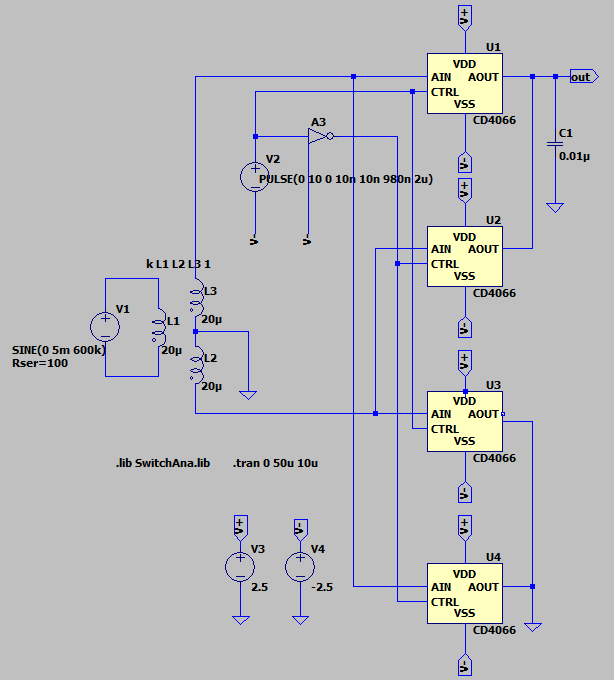
CMOSアナログスイッチとパルス発振回路を使えばこのような回路は簡単に構成できる。例えば、標準CMOSロジックの4066を使ってLTSpice上に組んだミキサ回路は以下のような物。4066のSPICEモデルはデフォルトのLTSpiceには含まれていないため、別記事にまとめた方法などにより別途組み込みが必要。今回はここに置かれているSwitchAna.Libを利用させてもらった。
- (.ascファイルのダウンロードはこちら)
RF信号としてV1に900kHzのサイン波を発生させトランスの一次側に入力し、トランスの二次側に互いに逆相となるRF信号を得ている。V2で発生させた1MHzパルスでアナログスイッチを切り替えることでRF信号の極性を入れ替え、+1と-1の乗算を行うのと同等の結果を得る。
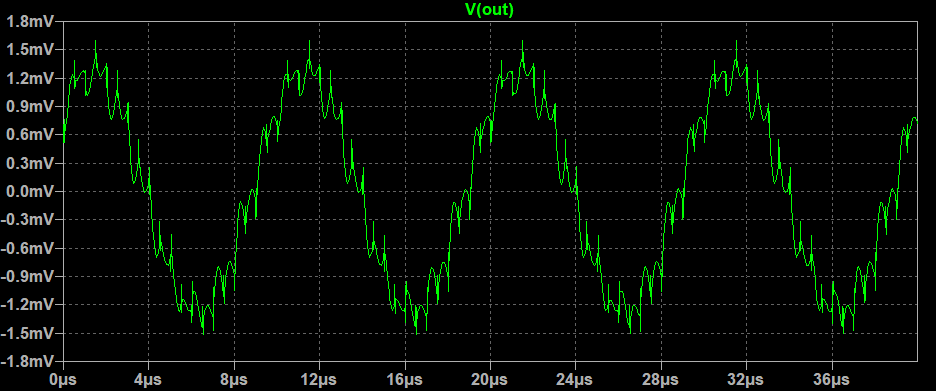
下のグラフはLTSpiceで上記回路の過渡解析(.tran解析)を行った結果。900kHzの信号がリップル状に残っているが、10us周期のサイン波、つまり100kHzが現れていることがわかる。
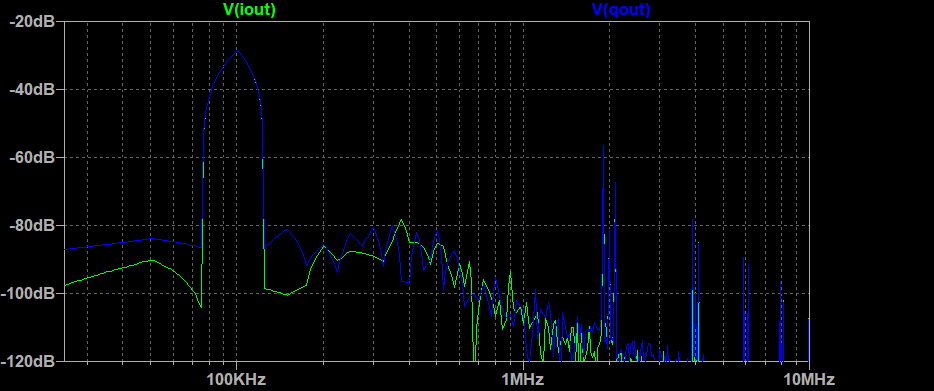
この波形をFFTした結果が下のグラフ。100kHzの信号が支配的だが、周波数変換前の元の信号成分である900Hzと1MHzのほか上の帯域に無数の高調波成分が見えている。これでも回路図中のコンデンサC1によるローパスフィルタ効果で不要な高域成分がある程度は除去出来ているのだが、場合によっては更にローパスフィルタをかけて除去する必要があるだろう。
IQ信号について
実用的な回路としては、上記のシンプルな周波数変換回路よりもIQ信号を出力する直交ミキサ回路(後述)の方がよく用いられているようだ。IQ信号の定義の仕方は色々あるようだが、当記事ではI信号が実部でQ信号が虚部の複素信号と考えることにする。
複素信号を扱う上でまず知っておくべきは、複素正弦波だ。周波数fの複素正弦波は以下のように実部がコサイン波で虚部がサイン波という信号(オイラーの公式)。直交ミキサ回路ではこの複素正弦波を活用する。
{\rm e}^{2 \pi j f t} = \cos(2 \pi f t) + j \sin(2 \pi f t)複素正弦波を導入するメリットの一つは「周波数の正負が表現出来る」ことだろう。周波数に符号を付けるなんてピンと来ないかもしれないが、実信号である実正弦波は周波数の符号が反転した複素正弦波2本の合成で表現する事が出来るのだ。
\cos(2 \pi f t) = \frac{{\rm e}^{2 \pi j f t} + {\rm e}^{-2 \pi j f t} }{2}実正弦波を2本の複素正弦波の合成で表現すると、周波数変換回路で複素正弦波を使うメリットも理解しやすい。実正弦波は正負の周波数成分を必ず両方持つのに対して、複素正弦波は正か負いずれかの周波数成分だけを持つ。「正負いずれかの周波数成分だけを持つ」というのが大事なポイントで、この性質によって直交ミキサでは周波数変換を正方向もしくは負方向への単純な周波数シフトとすることが出来る。複素信号と聞くとややこしそうだが、実信号で行うと面倒なことになる周波数変換を、複素信号を用いた直交ミキサでは寧ろシンプルに出来るのだ。
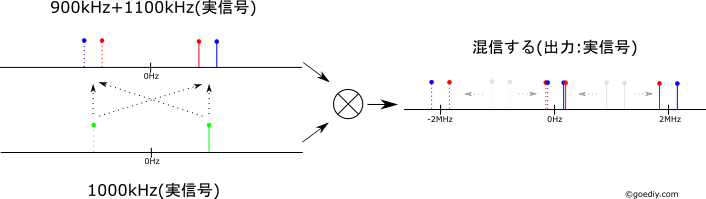
以下、900kHzと1100kHzの実正弦波で構成されたRF信号に1000kHzの実正弦波を乗算した場合と複素正弦波を乗算した場合とを比較する。数式で説明した方が見通しが良い面もあるが、趣味のブログに数式は馴染まないので割愛する。とはいえ、興味のある人は自身で数式を書き下すとより理解が深まると思う。
実正弦波を乗算
1000kHzの実正弦波をRF信号に乗算すると、900kHzも1100kHzも同じ100kHzに変換されて混信してしまう。この原因は、1000kHzの実正弦波には周波数が1000kHzと-1000kHzの複素正弦波が含まれており、それらとRF信号がグチャグチャに相互作用する結果として混信が発生するというのがざっくりとした説明だ(下の複素正弦波の説明を注意深く読むと、その原因も理解出来る筈)。
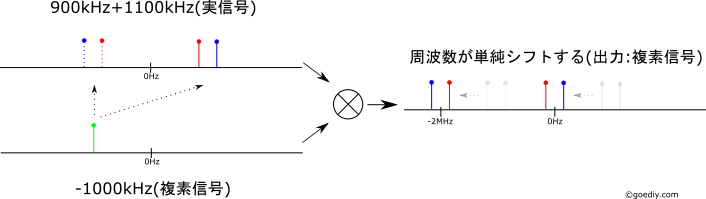
負周波数の複素正弦波を乗算
-1000kHzの複素正弦波を乗算して周波数変換すると単純な-1000kHzの周波数シフトとなり、混信させることなく-100kHzと100kHzのサイン波を得る事が出来る
-1900kHzと-2100kHzも生成されるが、これはフィルタで除去すれば良い。
正周波数の複素正弦波を乗算
正の周波数である+1000kHzの複素正弦波を乗算すると、上記の例とは反対に正の周波数方向へのシフトとなる。
1900kHzと2100kHzも生成されるが、これも上記と同様フィルタで除去すれば良い。
正負周波数の乗算結果を重ねると…
正の周波数の複素数正弦波を乗算した結果と負の周波数の複素数正弦波を乗算した結果を足し合わせると、実正弦波を乗算した結果と同じになる事が分かるだろう。
CMOSアナログスイッチを用いた直交ミキサ回路
直交ミキサは、前節で説明した通り複素正弦波をRF信号に乗算する回路だ。複素正弦波は実部がコサイン波で虚部がサイン波の信号であり、コサイン波とサイン波をそれぞれ乗算する2つのミキサ回路があれば作ることが出来る。やや専門的(かつ英語)ではあるが、この直交ミキサをアナログスイッチで作る方法は以下の文献で紹介されている。
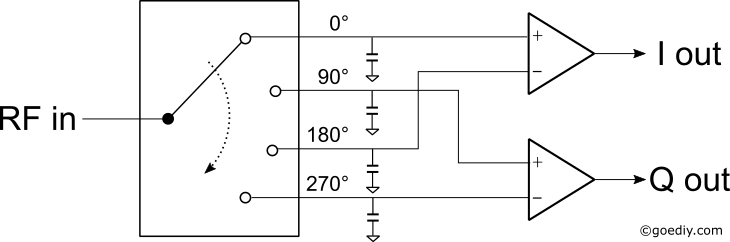
この文献に書かれたアナログスイッチによる直交ミキサは、以下の図のような物。
この回路を少しアレンジし、180°と270°の積分を省略して0°と90°の積分だけを行う簡易版の回路はネットでよく見かける(例えば、このサイトで公開されている回路)。
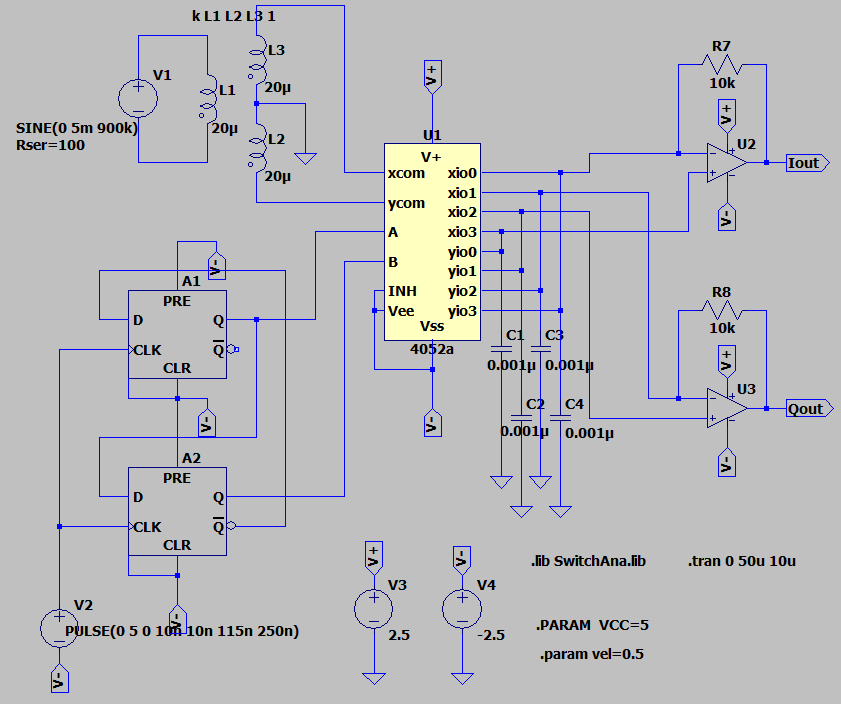
標準CMOSロジックの4052を用いてLTSpice上で組んだ直交ミキサは以下の回路。4052のSPICEモデルは4066と同じくここに置かれているSwitchAna.Libの中で定義されている物を利用させてもらった(4052のSPICEモデルはVCCやナゾのvelというパラメータを.paramディレクティブで設定が必要)。
- (.ascファイルのダウンロードはこちら)
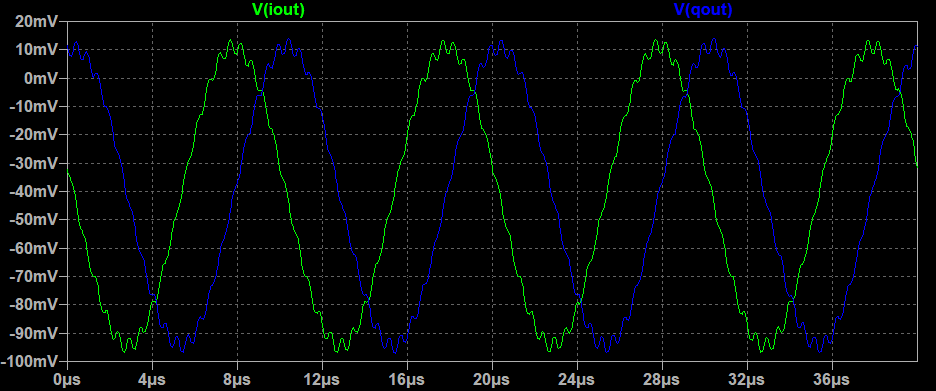
この回路で過渡解析(tran解析)を実行すると、期待通りに90°位相がずれた100kHzの正弦波がIQ信号として得られる。4066を用いた周波数変換回路と比較するとギザギザした不要な成分が少なめで、オペアンプによる増幅回路が後段に付いているため出力信号の振幅も大きい。ただ何故かDCオフセットが付いているが、原因はよくわからない。
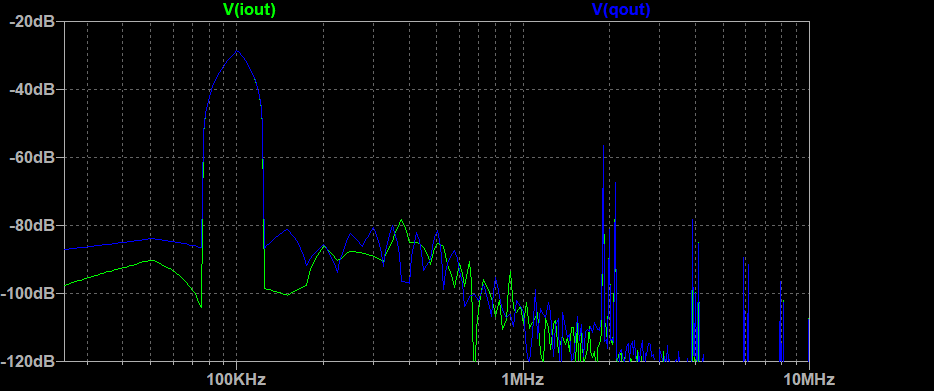
この信号をFFT解析した結果は以下。LTSpiceでは複素信号を扱うことが出来ないため残念ながら100kHzの正弦波が単に2つ得られているだけのグラフになっているが、この信号をIQ信号として複素FFTすると負の周波数成分を持たない100kHzの正弦波となる筈だ。
まとめ
以前からCMOSアナログスイッチを用いた周波数変換回路について聞きかじってはいたが、その原理など詳細は知らなかった。そしていざネットで調べてみても断片的な情報が多く、IQ出力の回路図を見てもチンプンカンプンだったが、海外の専門的な文献も参照してようやく原理を理解出来たので自分としても非常に勉強になった。
またネットに上がっているIQ信号の解説はどれも自分には理解しにくいと感じたので、今回の記事では出来るだけ分かりやすく解説したつもりだ。今回の記事が直交ミキサの理解のために誰かの役に立てたら嬉しい。
理論を紐解くと色々奥深い要素がある直交ミキサだが、CMOSアナログスイッチとオペアンプといったありふれた部品で簡単に作ることが出来、LTSpiceのシミュレーションで動作を確認することが出来た。ただ今回行ったLTSpiceによるシミュレーションでは直交ミキサからIQ信号として複素信号を出力するメリットを示すことが出来なかった。この点については、SDRシリーズの記事で実際にGNURadio上にSDRを構築して解説する予定だ。



コメント